The Probabilistic Inference Challenge (PIC2011)

General

We are pleased to announce the PASCAL 2011 challenge for probabilistic inference in graphical models. Modelled after the UAI 2010 inference evaluation, the current challenge focuses on challenging models and covers a wider range of network categories with the goal of setting a new standard for the evaluation of probabilistic inference procedures.

The evaluation will assess performance of three inference tasks:

PR: Partition function.
MPE: Most probable explanation (also known as MAP or energy minimization).
MAR: Single node marginals.

For each task, submitted solvers will be evaluated in three different time regimes:

Speedy: up to 20 second
Lunch-break: up to 20 minutes
Take your time: up to 1 hour

Only network instances that can be processed by a simple asynchronous belief propagation procedure are included in each category.

The evaluation will not distinguish between exact and approximate algorithms. Each solver will have to declare the tasks it solves. A formal definition of the four tasks is given at the end of this document. A team can submit multiple solvers per task as long as the solvers are based on different algorithmic principles.

Evaluation Format

Our goal is to evaluate efficiency and approximation accuracy. Each solver is given problem instances consisting of:

A Markov network M (this may also be a moralized version of a directed model).
Values of observed variables (evidence) in the network e.
If the evidence is not provided it is assumed that no variables are observed.

A solver is expected to provide a solution (exact or approximate) for each problem instance, given constraints on time and space resources. Details of the evaluation process can be found here.

Execution Environment

The evaluations will be run on an AMD machine running Linux with up to 4 GB memory made available (some memory will be reserved for evaluation scripts, etc.). We request that solvers be 64-bit executables, using only a single core (i.e., no parallel processes/threads). A solver will have available the following environment variables:

INF_TIME: total CPU runtime limit (in seconds, e.g., "600");
INF_MEMORY: total memory limit (in gigabytes, e.g., "2.5");

The solver's exit status will be recorded, treating 0 as normal and other numbers as an error. Processes exceeding time or memory limits will be killed (via a SIGKILL signal), and the final output solution (see format below) will be taken as the solver solution. In case a solution is not available, a naive one (e.g. bit-wise univariate potential maximum for the MAP task) will be assumed.

Command-line Format

A solver will receive as input a filename of the model, a filename for the evidence, a seed, and the task to solve ( PR/ MPE/ MAR/ BEL):

./solver input-model-file input-evidence-file seed PR|MPE|MAR|BEL

We ask randomized algorithms to use an input seed, so that two runs of a solver, given the same input, will yield the same output in a comparable amount of time. Deterministic algorithms may ignore the seed.

Input format

The input model will be a Markov network defined as a set of factors (see formal definition below) specified in a simple text format. Evidence instances (one or more) will be provided in a simple variable-value pair format. A detailed description of the input formats along with examples can be found here. Note that this year solvers need to only handle Markov networks (although the given models may in some cases correspond to moralized Bayesian networks).

Output Format

The solver should generate a file and write the results to it. The output file should have the same name as the input model file, but with the added suffix ".XXX" where XXX is the task being solved (PR, MAR etc.). For example, after calling:

./solver Nets/grid5X5.uai Evid/grid5X5.uai.evid 35  PR

The solution should be found in the working directory in a file named grid5X5.uai.PR. Solver output to stdout and stderr will be logged, for debugging purposes.

A complete description of the result file format can be found here

Task Definitions

Notation

Every inference task is defined with respect to a set of discrete variables X = X₁ ,..., X_n. In what follows, we will use capital letters (X) to denote variables, and small letters (x) to denote their values. We will also use boldface capital letters (X) to denotes sets of variables, and boldface small letters (x) to denote instantiations {X₁ = x₁ ,..., X_n = x_n }. We will say that two variable instantiations y and z are compatible, written y∼z , if they agree on the value of every common variable in Y ∩ Z. A factor f_i (X_i), where X_i ⊆X,is a function that maps each instantiation x_i into a non-negative number, denoted f_i (x_i ).

Markov networks

Let G be a graph over variables X = X₁ ,..., X_n. Let X₁...X_m be a sets of variables, such that X_a ⊆ X for all a. A Markov network over G is a set of factors f₁ (X₁) ,..., f_n (X_n ).

A Markov network defines a joint factor (unnormalized probability)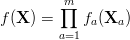

$f(\mathbf X) = \prod_{a=1}^m f_a(\mathbf X_a)$ .
The probability of an instance x is: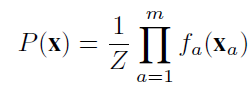

where Z, known as the (empty evidence) partition function is defined as:

An evidence e is an instantiation of a subset of variables in the network E ⊆ X. The following inference tasks are defined for a Markov network with joint factor f(X) and evidence e:

PR (partition function): compute the function
- $Pr(\mathbf e) = \sum_{\mathbf x \sim \mathbf e} f(\mathbf x)$ .
MPE (most probable explanation): compute the MPE instantiation
- $\mathbf x^* = {\arg\!\max}_{\mathbf x \sim \mathbf e}\, f(\mathbf x)$
MAR (node marginals): for each variable X_i and each of its values x_i , compute the marginal probabilities:
- $Pr(x_i\vert \mathbf e) = \frac {Pr(x_i,\mathbf e)} {Pr(\mathbf e)}$ .
BEL (cliques marginals): for each factor f_i and each assignment of its variables X_i, compute the marginal probability.
- $Pr(X_i\vert \mathbf e) = \frac {Pr(X_i,\mathbf e)} {Pr(\mathbf e)}$ .

| Contact admin |