Algorithms Ex9 – Solution

1. a.

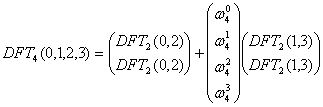
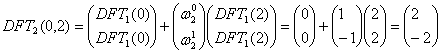
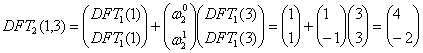
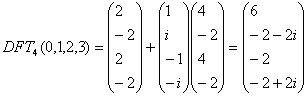
b.

1) The coefficient representation of the polynomials as degree-bound 2n:

2) We compute point-value representations of the polynomials:

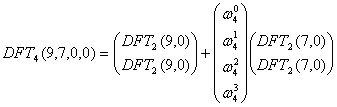
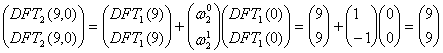
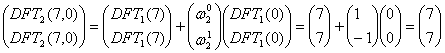
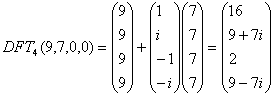
Similarly we compute

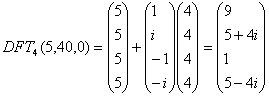
3) Point-wise multiplication:

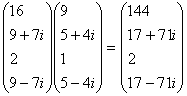
4) Interpolation:

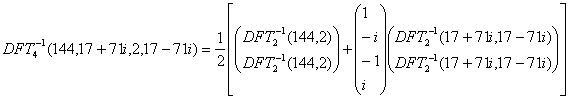
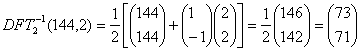
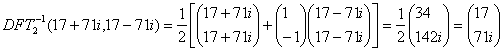
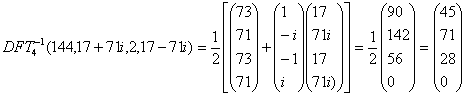
We’ll verify that by a regular multiplication:

■

2.

Define two polynomials and :

where if , otherwise.

where if , otherwise.

We’ll look at the polynomial whose the product of and :

, where .

Therefore, for each j:

, meaning that should be in S.

Run-time

a. Defining the polynomials and : We sort sets A and B : , then go through to compute the coefficients of and :

b. Multiplying the polynomials. Can be done through FFT in

c. Going through the coefficients of and adding to S each :

and totally: ■

3.

We assume the alphabet is {-1,1} or change every 0 to -1.

Define polynomials and for T and S-Reverse:

Multiply and through FFT:

, where . (if n<k, ).

is the sum of n+1 non-zero products (, and since and can be either 1 or -1 for each j, .

both and are 1 or both are -1 for every , , ... , , meaning a match was found.

We therefore return every index j-n, such that .

Run time:

a. Defining the polynomials is .

b. FFT: .

c. Checking which is

and totally: ■

4. We use the hint:has roots iff and show an algorithm that receives and returns the product in :

GetPoly ()

if (n=1) return

return FFT -Mul(GetPoly( , GetPoly()

Proof by induction:

Base: : The algorithm returns .

Assumption: Assume GetPoly(= 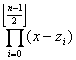and GetPoly(= .

Induction step:

The algorithm returns the product of the two above polynomials which by the assumption are:

= ■

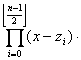
Complexity:

The recursion depth is and as the FFT multiplication takes we get .