Algorithms – Solutions to Exercise 8

Question 1

From the multinomial nature of the determinant we get:

.

By induction on n (the induction step is shown above and the proof for n=1 is trivial) we get .

Question 2

a.

We can get q(x) from p(x) by the simple long division algorithm that we use for numbers.

Each step in the algorithm is performed in O(1), and after each step we have p’(x) with 1 degree less à n steps are needed to finish the division.

Thus, the coefficients of polynomial q(x) given x0 can be computed in O(n).

b.

First, we’ll compute once the coefficients ofin O(n²).

Then, for each k=0..n-1 we’ll perform:

1.

Complexity is O(n) (multiplication of n-1 numbers)

2.

Complexity is O(n) as proven in (a).

Now we’ll add all the results and get with another O(n²).

The total complexity is O(n²).

Question 3

a.

We’ll use the interpolation polynomial as given by Lagrange’s formula:

b.

Again, we’ll use the interpolation polynomial as given by Lagrange’s formula:

Question 4

a.

The 8^th roots are:

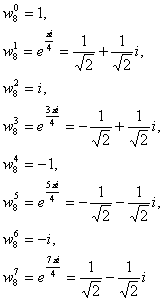
The 8^th primitive roots are . Proof is similar to (4b).

b.

If n is a prime number, then there are (n-1) primitive roots.

Proof: for each k, there exist x,y such that xk+yn=1. Then we have:

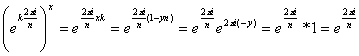
Question 5

a.

b.

Define a new matrix W:.

à W = I à .