Algorithms – Solutions to Exercise 2

Question 1

Pick an interval I. “Break the circle” at the starting point of I (we can throw all intervals that intersect I). Now use the Activity-Selector algorithm to find a set of non-intersecting intervals. The set we get is the largest set that contains I. To find the maximal set repeat the process for each of the intervals. Return the maximal set.

Question 2

A counter example for both cases:

Input lecture times: (1,5) (6,10) (1,7) (8,9).

Any algorithm that maximizes each room before opening another room after sorting by end time would choose for the first room the following lectures: (1,5) (8,9). Afterwards it’ll have to open 2 more rooms for the remaining 2 lectures. Both given algorithms will put the lectures in 3 rooms:

1: (1,5) (8,9)

2: (1,7)

3: (6,10)

While the optimal solution requires only 2 rooms:

1: (1,5) (6,10)

2: (1,7) (8,9)

Question 3

(a)

Solutions to the activity allocation problem don’t obey the exchange property. A counter example:

A = {(1,5) (6,10)}

B = {(1,10)}

Both subsets A and B are legal solutions for the activity allocation problem, and |A| > |B|, but there is no element b in B\A such that A and {b} is a legal solution.

à Solutions to the activity allocation problem are not a matroid.

(b) Solutions to the 0-1 knapsack problem don’t obey the exchange property too. A counter example (similar to the previous one):

A = {(1,5) (6,5)}

B = {(1,10)}

And suppose that the maximal NEFACH = 10.

Both subsets A and B are legal solutions for the 0-1 knapsack problem, and |A| > |B|, but there is no element b in B\A such that A and {b} is a legal solution.

à Solutions to the 0-1 knapsack problem are not a matroid.

Question 4

(a)

Suppose a₁ < a₂ < .. < a_n, and if not – sort them.

Then .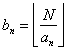

For each i=(n-1) … 1

.

The idea in the greedy algorithm is in each step to choose the biggest number b_i, without violating the constraint that .

(b)

It can be easily checked that for any solution {o_i} different from the greedy one, must occur one of the following:

• a subsequence of o₁*1+o₂*5 which is exactly 10 and then the proposed solution can be optimized by subtracting from o₁ and o₂ the relevant part and adding 1 to o₃ (coefficient of 10 in the solution)
• a subsequence of o₁*1 which is exactly 5 and then the proposed solution can be optimized by subtracting from o₁ the relevant part and adding 1 to o₂(coefficient of 10 in the solution)

(c)

Suppose that the greedy algorithm’s choice is {b_i}, and there exists an optimal solution {o_i} such that, but.

We’ll prove the contradiction by induction on N.

For N=1: b₁ = 1, and this solution is optimal.

Assume that for any number smaller than N the greedy algorithm gives the optimal solution and we’ll prove for N.

Let a_j=max{a_k : a_k <N} (the maximal power of a, which is still less than N).

Notice that if i<j then o_i < a, because otherwise we could decrease o_i by a and increase o_i+1 by 1, improving the optimal solution.

Now the greedy solution will try to enlarge b_j as much as possible. If in the optimal solution {o_i} o_j=b_j then the solution for is optimal from the induction assumption.

If in the optimal solution {o_i} o_j < b_j , we have

giving us

but we know that that if i<j then o_i < a, thus we have

contradiction!!!

(d)

If N=2k, take a₁ =1, a₂ =k, a₃ =k+1. The greedy solution is N=(k-1)* a₁+0* a₂+ 1* a₃

The solution N=0 *a₁+2* a₂+ 0* a₃ is better for k>2

If N=2k+1 take a₁ =1, a₂ =k, a₃ =k+2. The greedy solution is N=(k-1)* a₁+0* a₂+ 1* a₃

The solution N=1 *a₁+2* a₂+ 0* a₃ is better for k>3