nnls

Purpose

Nonnegative least squares.

Synopsis

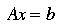
x = nnls(A,b)
x = nnls(A,b,tol)
[x,w] = nnls(A,b)
[x,w] = nnls(A,b,tol)

Description

x = nnls(A,b) solves the system of equations

in a least squares sense, subject to the constraint that the solution vector x have nonnegative elements

x = nnls(A,b,tol) specifies a tolerance tol, that determines when an element is less than 0. By default, tol is

max(size(A))*norm(A,1)*eps
[x,w] = nnls(...) returns the dual vector w. The elements of x and w are related by

Examples

Compare the unconstrained least squares solution to the nnls solution for a 4-by-2 problem:

A =
    0.0372    0.2869
    0.6861    0.7071
    0.6233    0.6245
    0.6344    0.6170
          
b =
    0.8587
    0.1781
    0.0747
    0.8405
          
[A\b nnls(A,b)] =
          
    -2.5625        0
     3.1106   0.6929
          
[norm(A*(a\b)-b) norm(A*nnls(a,b)-b)] =
         
    0.6677    0.9119
The solution from nnls does not fit as well, but has no negative components.

Algorithm

nnls uses the algorithm described in [1], Chapter 23. The algorithm starts with a set of possible basis vectors, computes the associated dual vector w, and selects the basis vector corresponding to the maximum value in w to swap out of the basis in exchange for another possible candidate, until w <= 0.

See Also

\

References

[1] C. L. Lawson and R. J. Hanson, Solving Least Squares Problems, Chapter 23, Prentice-Hall, 1974.

(c) Copyright 1994 by The MathWorks, Inc.