ellipke

Purpose

Complete elliptic integrals of the first and second kind.

Synopsis

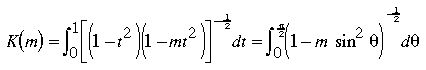
K = ellipke(m)
[K,E] = ellipke(m)

Description

[K,E] = ellipke(m) returns the complete elliptic integral of the first and second kinds for the elements of m. The complete elliptic integral of the first kind, K(m) = F(pi/2|m), is defined by

The complete elliptic integral of the second kind, E(m) = E(K(m)) = E(pi/2|m), is defined by

Some definitions of K and E use the modulus k instead of the parameter m. They are related by

The accuracy of the result is eps; the value of eps can be changed for a less accurate, but more quickly computed answer.

Algorithm

The complete elliptic integral is computed using the method of the arithmetic-geometric mean described in [1], section 17.6. Start with the triplet of numbers:

Compute successive iterations of ai, bi, and ci with

stopping at iteration n when cn \xc5 0, within the tolerance specified by eps. The complete elliptic integral of the first kind is then

Limitations

ellipke is limited to the input domain 0 <= m<= 1.

References

[1] M. Abramowitz and I.A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, 17.6.